Mathematics
Rationale
Learning mathematics creates opportunities for and enriches the lives of all Australians. The Western Australian Curriculum: Mathematics provides students with essential mathematical skills and knowledge in Number and Algebra, Measurement and Geometry, and Statistics and Probability. It develops the numeracy capabilities that all students need in their personal, work and civic life, and provides the fundamentals on which mathematical specialties and professional applications of mathematics are built.
Mathematics has its own value and beauty and the Western Australian Curriculum: Mathematics aims to instil in students an appreciation of the elegance and power of mathematical reasoning. Mathematical ideas have evolved across all cultures over thousands of years, and are constantly developing. Digital technologies are facilitating this expansion of ideas and providing access to new tools for continuing mathematical exploration and invention. The curriculum focuses on developing increasingly sophisticated and refined mathematical understanding, fluency, logical reasoning, analytical thought and problem-solving skills. These capabilities enable students to respond to familiar and unfamiliar situations by employing mathematical strategies to make informed decisions and solve problems efficiently.
The Western Australian Curriculum: Mathematics ensures that the links between the various components of mathematics, as well as the relationship between mathematics and other disciplines, are made clear. Mathematics is composed of multiple but interrelated and interdependent concepts and systems which students apply beyond the mathematics classroom. In science, for example, understanding sources of error and their impact on the confidence of conclusions is vital, as is the use of mathematical models in other disciplines. In geography, interpretation of data underpins the study of human populations and their physical environments; in Humanities and Social Sciences, students need to be able to imagine timelines and time frames to reconcile related events; and in English, deriving quantitative and spatial information is an important aspect of making meaning of texts.
The curriculum anticipates that schools will ensure all students benefit from access to the power of mathematical reasoning and learn to apply their mathematical understanding creatively and efficiently. The mathematics curriculum provides students with carefully paced, in-depth study of critical skills and concepts. It encourages teachers to help students become self-motivated, confident learners through inquiry and active participation in challenging and engaging experiences.
Aims
The Western Australian Curriculum: Mathematics aims to ensure that students:
- are confident, creative users and communicators of mathematics, able to investigate, represent and interpret situations in their personal and work lives and as active citizens
- develop an increasingly sophisticated understanding of mathematical concepts and fluency with processes, and are able to pose and solve problems and reason in Number and Algebra, Measurement and Geometry, and Statistics and Probability
- recognise connections between the areas of mathematics and other disciplines and appreciate mathematics as an accessible and enjoyable discipline to study.
Content Structure
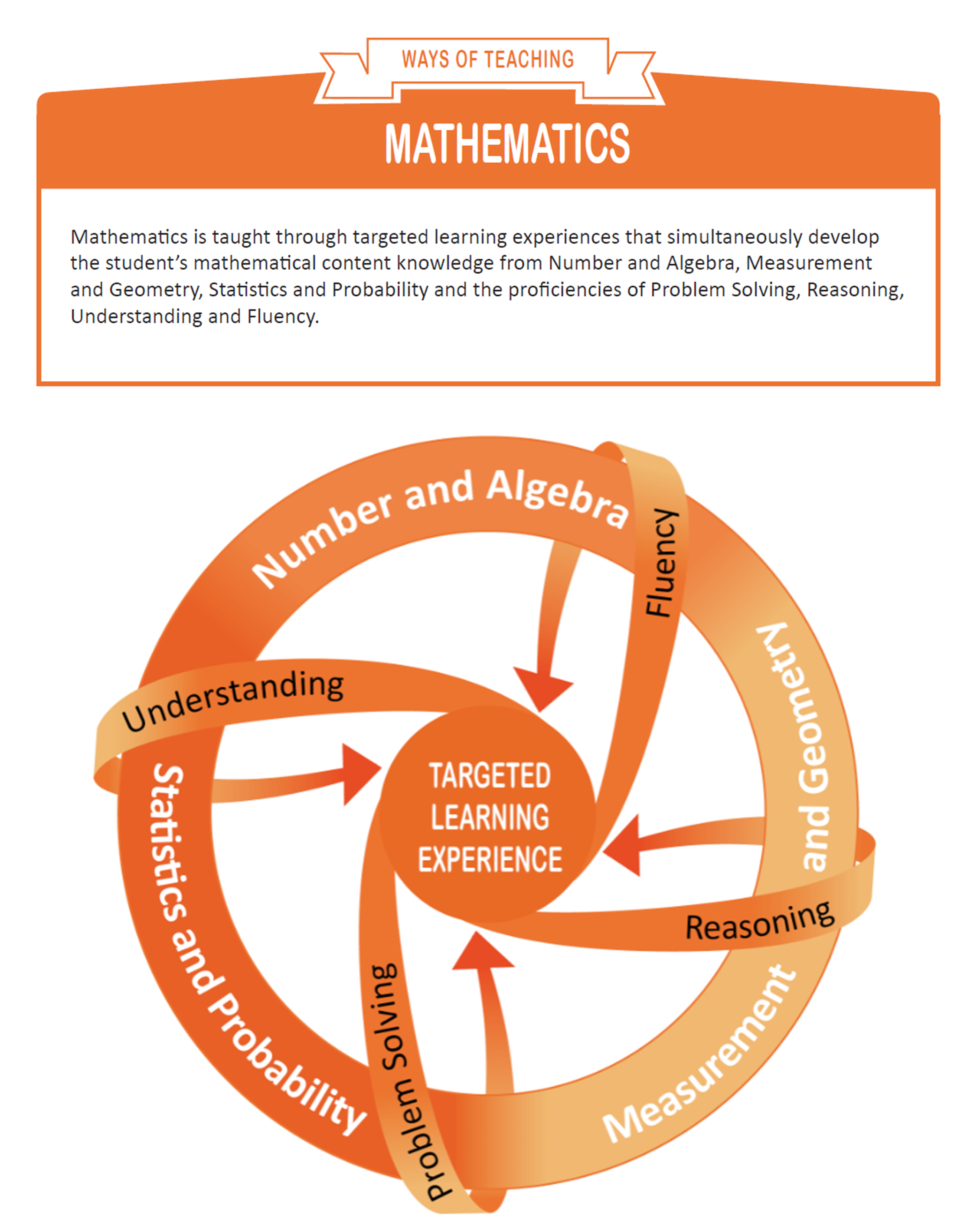
The Western Australian Curriculum: Mathematics is organised around the interaction of three content strands and four proficiency strands.
The content strands are Number and Algebra, Measurement and Geometry, and Statistics and Probability. They describe what is to be taught and learnt.
The proficiency strands are Understanding, Fluency, Problem Solving, and Reasoning. They describe how content is explored or developed, that is, the thinking and doing of mathematics. They provide the language to build in the developmental aspects of the learning of mathematics and have been incorporated into the content descriptions of the three content strands described above. This approach has been adopted to ensure students' proficiency in mathematical skills develops throughout the curriculum and becomes increasingly sophisticated over the years of schooling.
Content strands
Number and Algebra
Number and Algebra are developed together, as each enriches the study of the other. Students apply number sense and strategies for counting and representing numbers. They explore the magnitude and properties of numbers. They apply a range of strategies for computation and understand the connections between operations. They recognise patterns and understand the concepts of variable and function. They build on their understanding of the number system to describe relationships and formulate generalisations. They recognise equivalence and solve equations and inequalities. They apply their number and algebra skills to conduct investigations, solve problems and communicate their reasoning.
Measurement and Geometry
Measurement and Geometry are presented together to emphasise their relationship to each other, enhancing their practical relevance. Students develop an increasingly sophisticated understanding of size, shape, relative position and movement of two-dimensional figures in the plane and three-dimensional objects in space. They investigate properties and apply their understanding of them to define, compare and construct figures and objects. They learn to develop geometric arguments. They make meaningful measurements of quantities, choosing appropriate metric units of measurement. They build an understanding of the connections between units and calculate derived measures such as area, speed and density.
Statistics and Probability
Statistics and Probability initially develop in parallel and the curriculum then progressively builds the links between them. Students recognise and analyse data and draw inferences. They represent, summarise and interpret data and undertake purposeful investigations involving the collection and interpretation of data. They assess likelihood and assign probabilities using experimental and theoretical approaches. They develop an increasingly sophisticated ability to critically evaluate chance and data concepts and make reasoned judgments and decisions, as well as building skills to critically evaluate statistical information and develop intuitions about data.
Proficiency strands
The proficiency strands describe the actions in which students can engage when learning and using the content. While not all proficiency strands apply to every content description, they indicate the breadth of mathematical actions that teachers can emphasise.
Understanding
Students build a robust knowledge of adaptable and transferable mathematical concepts. They make connections between related concepts and progressively apply the familiar to develop new ideas. They develop an understanding of the relationship between the 'why' and the 'how' of mathematics. Students build understanding when they connect related ideas, when they represent concepts in different ways, when they identify commonalities and differences between aspects of content, when they describe their thinking mathematically and when they interpret mathematical information.
Fluency
Students develop skills in choosing appropriate procedures, carrying out procedures flexibly, accurately, efficiently and appropriately, and recalling factual knowledge and concepts readily. Students are fluent when they calculate answers efficiently, when they recognise robust ways of answering questions, when they choose appropriate methods and approximations, when they recall definitions and regularly use facts, and when they can manipulate expressions and equations to find solutions.
Problem Solving
Students develop the ability to make choices, interpret, formulate, model and investigate problem situations, and communicate solutions effectively. Students formulate and solve problems when they use mathematics to represent unfamiliar or meaningful situations, when they design investigations and plan their approaches, when they apply their existing strategies to seek solutions, and when they verify that their answers are reasonable.
Reasoning
Students develop an increasingly sophisticated capacity for logical thought and actions, such as analysing, proving, evaluating, explaining, inferring, justifying and generalising. Students are reasoning mathematically when they explain their thinking, when they deduce and justify strategies used and conclusions reached, when they adapt the known to the unknown, when they transfer learning from one context to another, when they prove that something is true or false and when they compare and contrast related ideas and explain their choices.
Content descriptions
The mathematics curriculum includes content descriptions at each year level. These describe the knowledge, concepts, skills and processes that teachers are expected to teach and students are expected to learn. However, they do not prescribe approaches to teaching. The content descriptions are intended to ensure that learning is appropriately ordered and that unnecessary repetition is avoided. However, a concept or skill introduced at one year level may be revisited, strengthened and extended at later year levels as needed.
Sub-strands
Content descriptions are grouped into sub-strands to illustrate the clarity and sequence of development of concepts through and across the year levels. They support the ability to see the connections across strands and the sequential development of concepts from Pre-primary to Year 10.
| Number and Algebra | Measurement and Geometry | Statistics and Probability |
|---|---|---|
| Number and place value (P-8) | Using units of measurement (P-10) | Chance (1-10) |
| Fractions and decimals (1-6) | Shape (P-7) | Data representation and interpretation (P-10) |
| Real numbers (7-10) | Geometric reasoning (3-10) | |
| Money and financial mathematics (1-10) | Location and transformation (P-7) | |
| Patterns and algebra (P-10) | Pythagoras and trigonometry (9-10) | |
| Linear and non-linear relationships (7-10) |
Year level descriptions
Year level descriptions emphasise the importance of working mathematically within the content. They provide an overview of the relationship between the proficiencies (Understanding, Fluency, Problem Solving and Reasoning) and the content for each year level.
Content elaborations
Content elaborations are provided for Pre-primary to Year 10 to illustrate and exemplify content and assist teachers to develop a common understanding of the content descriptions. They are not intended to be comprehensive content points that all students need to be taught.
Ways of Teaching
The 'Ways of Teaching' supports teachers to plan curriculum delivery across the phases of learning. The teaching in each year should acknowledge and extend learning from previous years.
The 'Ways of Teaching' complements the principles of teaching and learning in the Western Australian Curriculum and Assessment Outline (http://k10outline.scsa.wa.edu.au/). The principles focus on the provision of a school and class environment that is intellectually, socially and physically supportive of learning. The principles assist whole-school planning and individual classroom practice. All students are given the opportunity to achieve the standard at their current year level, whilst teachers identify and implement appropriate interventions to support students’ progress towards this standard.
The three content strands of Number and Algebra, Measurement and Geometry, and Statistics and Probability together with the four proficiency strands of Problem Solving, Reasoning, Understanding and Fluency define the mandated Western Australian Mathematics Curriculum. The proficiencies describe how the content is to be explored and taught and should be developed simultaneously with the content. The four proficiency strands describe the actions of the thinking and doing of
Mathematics. These together with the mathematical content become increasingly sophisticated as students’ progress from Pre-Primary to Year 10.
Teaching Mathematics is about making connections to existing knowledge in order to solve new problems both within and beyond mathematics. It is about showing students the power and beauty of Mathematics and its relevance to the real world. Students must engage with both the content and the proficiencies in order to become flexible, creative and critical problem solvers and mathematical thinkers of the 21st century.
Programs are planned to ensure:
- content and proficiency strands are developed simultaneously
- major conceptual ideas from the current year syllabus are central to teacher programming
- all learning experiences within the program are purposeful, developmentally appropriate, and support the long-term learning outcomes
- connections are made between the year level content and past and future learning
- prior knowledge is taken into account and is extended
- appropriate planned interventions support students’ progress towards the achievement standard where required
- transferable skills and thinking processes are developed through problem solving
- activities are accessible and challenging to all students, providing opportunities for inclusivity and differentiation
- the literacy of Mathematics (language, graphics, symbols) is developed
- appropriate materials, models, images or other representations are used purposefully to support students to move towards abstract ideas and create new knowledge and strategies
- opportunities are created to allow students to communicate and justify their strategies and solutions
- the relevant general capabilities and the cross-curriculum priorities are incorporated to assist students to live and work successfully in the 21st century
Targeted learning experiences are created so that students:
- value and develop the behaviours described in the proficiencies
- represent, solve or explore meaningful and unfamiliar problems and situations
- have time to think about and engage with problem situations, making sense of new concepts, ideas and experiences
- apply learning from one problem to other problems that involve different scenarios or contexts
- build and select from a repertoire of strategies to address learning tasks
- have purposeful opportunities to work independently and collaboratively
- answer focused questions and participate in guided mathematical conversations that deepen thinking, strengthen understanding and lead to generalisations
- comprehend and communicate ideas using appropriate mathematical language
- understand the purpose and intent of the learning activity and, if appropriate, its connection to the real world
- are accountable and responsible for their learning
- confidently seek and act upon constructive feedback
- reflect on learning experiences to consolidate learning
- feel safe to take risks in their learning, develop resilience and explore mathematical ideas with curiosity
Mathematics across Pre-primary to Year 12
Although the curriculum is described year by year, this document provides advice across four year groupings on the nature of learners and the relevant curriculum:
- Pre-primary – Year 2: typically students from 5 to 8 years of age
- Years 3–6: typically students from 8 to 12 years of age
- Years 7–10: typically students from 12 to 15 years of age
- Senior secondary years: typically students from 15 to 18 years of age.
Pre-primary – Year 2
The early years (5–8 years of age) lay the foundation for learning mathematics. Students at this level can access powerful mathematical ideas relevant to their current lives and learn the language of mathematics, which is vital to future progression.
Children have the opportunity to access mathematical ideas by developing a sense of number, order, sequence and pattern; by understanding quantities and their representations; by learning about attributes of objects and collections, position, movement and direction, and by developing an awareness of the collection, presentation and variation of data and a capacity to make predictions about chance events.
Understanding and experiencing these concepts in the early years provides a foundation for algebraic, statistical and multiplicative thinking, that will develop in subsequent years. These foundations also enable children to pose basic mathematical questions about their world, to identify simple strategies to investigate solutions, and to strengthen their reasoning to solve personally meaningful problems.
Years 3–6
These years emphasise the importance of students studying coherent, meaningful and purposeful mathematics that is relevant to their lives. Students still require active experiences that allow them to construct key mathematical ideas, but also gradually move to using models, pictures and symbols to represent these ideas.
The curriculum develops key understandings by extending the number, measurement, geometric and statistical learning from the early years; by building foundations for future studies through an emphasis on patterns that lead to generalisations; by describing relationships from data collected and represented; by making predictions; and by introducing topics that represent a key challenge in these years, such as fractions and decimals.
In these years of schooling, it is particularly important for students to develop a deep understanding of whole numbers to build reasoning in fractions and decimals and to develop a conceptual understanding of place value. These concepts allow students to develop proportional reasoning and flexibility with number through mental computation skills, and to extend their number sense and statistical fluency.
Years 7–10
These years of school mark a shift in mathematics learning to more abstract ideas. Through key activities such as the exploration, recognition and application of patterns, the capacity for abstract thought can be developed and the ways of thinking associated with abstract ideas can be illustrated.
The foundations built in previous years prepare students for this change. Previously established mathematical ideas can be drawn upon in unfamiliar sequences and combinations to solve non-routine problems and to consequently develop more complex mathematical ideas. However, students of this age also need an understanding of the connections between mathematical concepts and their application in their world as a motivation to learn. This means using contexts directly related to topics of relevance and interest to this age group.
During these years, students need to be able to represent numbers in a variety of ways; to develop an understanding of the benefits of algebra, through building algebraic models and applications and the various applications of geometry; to estimate and select appropriate units of measure; to explore ways of working with data to allow a variety of representations; and to make predictions about events based on their observations.
The intent of the curriculum is to encourage the development of important ideas in more depth, and to promote the interconnectedness of mathematical concepts. An obvious concern is the preparation of students intending to continue studying mathematics in the senior secondary years. Teachers will, in implementing the curriculum, extend the more mathematically able students by using appropriate challenges and extensions within available topics. A deeper understanding of mathematics in the curriculum enhances a student's potential to use this knowledge to solve non-routine problems, both at this level of study and at later stages.
The 10A content is optional and is intended for students who require more content to enrich their mathematical study whilst completing the common Year 10 content. It is NOT anticipated that all students will attempt the 10A content, but doing so would be advantageous for students intending to pursue Mathematical Methods or Mathematics Specialist in the senior secondary years. A selection of topics from the 10A curriculum can be completed according to the needs of the students.
It is anticipated that all students will study the Western Australian Curriculum: Mathematics up to the end of Year 10. From Year 10, the curriculum should provide pathway options suitable for students of differing abilities and interests, and with a range of future career and study plans.
Senior secondary years
Four mathematics courses have been designed for the senior secondary years. They have been designed to allow flexibility for students, taking into account a range of future pathways and the reality that some students reassess their choice of mathematics program part way through the senior secondary years.
The elements of the content strands from Pre-primary to Year 10 are evident in the senior secondary curriculum, but are not used as the major organisers. The proficiency strands of Understanding, Fluency, Reasoning and Problem Solving are integrated into the content descriptions as in the Pre-primary to Year 10 curriculum.
Achievement Standards
Across Pre-primary to Year 10, achievement standards indicate the quality of learning students should typically demonstrate by a particular point in their schooling. Achievement standards comprise a written description and student work samples.
An achievement standard describes the quality of learning (the extent of knowledge, the depth of understanding and the sophistication of skills) that would indicate the student is well placed to commence the learning required at the next level of achievement.
The sequence of achievement standards across Pre-primary to Year 10 describes progress in the learning area. This sequence provides teachers with a framework of growth and development in the learning area.
Student work samples play a key role in communicating expectations described in the achievement standards. Each work sample includes the relevant assessment task, the student's response, and annotations identifying the quality of learning evident in the student's response in relation to relevant parts of the achievement standard.
Together, the description of the achievement standard and the accompanying set of annotated work samples help teachers to make judgments about whether students have achieved the standard.
Student diversity
The School Curriculum and Standards Authority is committed to the development of a high-quality curriculum for all Australian students that promotes excellence and equity in education.
All students are entitled to rigorous, relevant and engaging learning programs drawn from the Western Australian Curriculum: Mathematics. Teachers take account of the range of their students' current levels of learning, strengths, goals and interests and make adjustments where necessary. The three-dimensional design of the Western Australian Curriculum, comprising learning areas, general capabilities and cross-curriculum priorities, provides teachers with flexibility to cater for the diverse needs of students across Australia and to personalise their learning.
More detailed advice has been developed for schools and teachers on using the Western Australian Curriculum to meet diverse learning needs and is available under Student Diversity on the Australian Curriculum website.
Students with disability
The Disability Discrimintion Act 1992 and the Disability Standards for Education 2005 require education and training service providers to support the rights of students with disability to access the curriculum on the same basis as students without disability.
Many students with disability are able to achieve educational standards commensurate with their peers, as long as the necessary adjustments are made to the way in which they are taught and to the means through which they demonstrate their learning.
In some cases curriculum adjustments are necessary to provide equitable opportunities for students to access age-equivalent content in the Western Australian Curriculum: Mathematics. Teachers can draw from content at different levels along the Pre-primary to Year 10 sequence. Teachers can also use the extended general capabilities learning continua in Literacy, Numeracy and Personal and social capability to adjust the focus of learning according to individual student need.
Gifted and talented students
Teachers can use the Western Australian Curriculum: Mathematics flexibly to meet the individual learning needs of gifted and talented students.
Teachers can enrich student learning by providing students with opportunities to work with learning area content in more depth or breadth; emphasising specific aspects of the general capabilities learning continua (for example, the higher order cognitive skills of the Critical and creative thinking capability); and/or focusing on cross-curriculum priorities. Teachers can also accelerate student learning by drawing on content from later levels in the Western Australian Curriculum: Mathematics and/or from local state and territory teaching and learning materials.
English as an additional language or dialect
Students for whom English is an additional language or dialect (EAL/D) enter Australian schools at different ages and at different stages of English language learning and have various educational backgrounds in their first languages. Whilst many EAL/D students bring already highly developed literacy (and numeracy) skills in their own language to their learning of Standard Australian English, there is a significant number of students who are not literate in their first language, and have had little or no formal schooling.
While the aims of the Western Australian Curriculum: Mathematics are the same for all students, EAL/D students must achieve these aims while simultaneously learning a new language and learning content and skills through that new language. These students may require additional time and support, along with teaching that explicitly addresses their language needs. Students who have had no formal schooling will need additional time and support in order to acquire skills for effective learning in formal settings.
General capabilities
In the Western Australian Curriculum, the general capabilities encompass the knowledge, skills, behaviours and dispositions that, together with curriculum content in each learning area and the cross-curriculum priorities, will assist students to live and work successfully in the twenty-first century.
There are seven general capabilities:
- Literacy
- Numeracy
- Information and communication technology (ICT) capability
- Critical and creative thinking
- Personal and social capability
- Ethical understanding
- Intercultural understanding.
In the Western Australian Curriculum: Mathematics, general capabilities are identified wherever they are developed or applied in content descriptions. They are also identified where they offer opportunities to add depth and richness to student learning through content elaborations. Icons indicate where general capabilities have been identified in Mathematics content. Teachers may find further opportunities to incorporate explicit teaching of the capabilities depending on their choice of activities.
Literacy
Students become literate as they develop the knowledge, skills and dispositions to interpret and use language confidently for learning and communicating in and out of school and for participating effectively in society. Literacy involves students in listening to, reading, viewing, speaking, writing and creating oral, print, visual and digital texts, and using and modifying language for different purposes in a range of contexts.
Literacy is an important aspect of mathematics. Students develop literacy in mathematics as they learn the vocabulary associated with number, space, measurement and mathematical concepts and processes. This vocabulary includes synonyms (minus, subtract), technical terminology (digits, lowest common denominator), passive voice (If 7 is taken from 10) and common words with specific meanings in a mathematical context (angle, area). They develop the ability to create and interpret a range of texts typical of mathematics ranging from calendars and maps to complex data displays.
Students use literacy to understand and interpret word problems and instructions that contain the particular language features of mathematics. They use literacy to pose and answer questions, engage in mathematical problem solving, and to discuss, produce and explain solutions.
Numeracy
Students become numerate as they develop the knowledge and skills to use mathematics confidently across all learning areas at school and in their lives more broadly. Numeracy involves students in recognising and understanding the role of mathematics in the world and having the dispositions and capacities to use mathematical knowledge and skills purposefully.
Mathematics has a central role in the development of numeracy in a manner that is more explicit and foregrounded than is the case in other learning areas. It is important that the Mathematics curriculum provides the opportunity to apply mathematical understanding and skills in context, both in other learning areas and in real world contexts. A particularly important context for the application of Number and Algebra is financial mathematics. In Measurement and Geometry, there is an opportunity to apply understanding to design. The twenty-first century world is information driven, and through Statistics and Probability students can interpret data and make informed judgments about events involving chance.
Information and Communication Technology (ICT) capability
Students develop ICT capability as they learn to use ICT effectively and appropriately to access, create and communicate information and ideas, solve problems and work collaboratively in all learning areas at school, and in their lives beyond school. ICT capability involves students in learning to make the most of the technologies available to them, adapting to new ways of doing things as technologies evolve and limiting the risks to themselves and others in a digital environment.
Students develop ICT capability when they investigate, create and communicate mathematical ideas and concepts using fast, automated, interactive and multimodal technologies. They employ their ICT capability to perform calculations, draw graphs, collect, manage, analyse and interpret data; share and exchange information and ideas and investigate and model concepts and relationships.
Digital technologies, such as spreadsheets, dynamic geometry software and computer algebra software, can engage students and promote understanding of key concepts.
Critical and creative thinking
Students develop capability in critical and creative thinking as they learn to generate and evaluate knowledge, clarify concepts and ideas, seek possibilities, consider alternatives and solve problems. Critical and creative thinking are integral to activities that require students to think broadly and deeply using skills, behaviours and dispositions such as reason, logic, resourcefulness, imagination and innovation in all learning areas at school and in their lives beyond school.
Students develop critical and creative thinking as they learn to generate and evaluate knowledge, ideas and possibilities, and use them when seeking solutions. Engaging students in reasoning and thinking about solutions to problems and the strategies needed to find these solutions are core parts of the Mathematics curriculum.
Students are encouraged to be critical thinkers when justifying their choice of a calculation strategy or identifying relevant questions during a statistical investigation. They are encouraged to look for alternative ways to approach mathematical problems, for example, identifying when a problem is similar to a previous one, drawing diagrams or simplifying a problem to control some variables.
Personal and social capability
Students develop personal and social capability as they learn to understand themselves and others, and manage their relationships, lives, work and learning more effectively. The personal and social capability involves students in a range of practices including recognising and regulating emotions, developing empathy for and understanding of others, establishing positive relationships, making responsible decisions, working effectively in teams and handling challenging situations constructively.
Students develop and use personal and social capability as they apply mathematical skills in a range of personal and social contexts. This may be through activities that relate learning to their own lives and communities, such as time management, budgeting and financial management, and understanding statistics in everyday contexts.
The Mathematics curriculum enhances the development of students' personal and social capabilities by providing opportunities for initiative taking, decision making, communicating their processes and findings, and working independently and collaboratively in the mathematics classroom.
Ethical understanding
Students develop ethical understanding as they identify and investigate the nature of ethical concepts, values, character traits and principles, and understand how reasoning can assist ethical judgment. Ethical understanding involves students in building a strong personal and socially oriented ethical outlook that helps them to manage context, conflict and uncertainty, and to develop an awareness of the influence that their values and behaviour have on others.
There are opportunities in the Mathematics curriculum to explore, develop and apply ethical understanding in a range of contexts, for example through analysing data and statistics; seeking intentional and accidental distortions; finding inappropriate comparisons and misleading scales when exploring the importance of fair comparison; and interrogating financial claims and sources.
Intercultural understanding
Students develop intercultural understanding as they learn to value their own cultures, languages and beliefs, and those of others. They come to understand how personal, group and national identities are shaped, and the variable and changing nature of culture. The capability involves students in learning about and engaging with diverse cultures in ways that recognise commonalities and differences, create connections with others and cultivate mutual respect.
Intercultural understanding can be enhanced in Mathematics when students are exposed to a range of cultural traditions. Students learn to understand that mathematical expressions use universal symbols, while mathematical knowledge has its origin in many cultures. Students realise that proficiencies such as understanding, fluency, reasoning and problem solving are not culture or language specific, but that mathematical reasoning and understanding can find different expression in different cultures and languages. New technologies and digital learning environments provide interactive contexts for exploring mathematical problems from a range of cultural perspectives and within diverse cultural contexts. Students can apply mathematical thinking to identify and resolve issues related to living with diversity.
Cross-curriculum priorities
The Western Australian Curriculum is designed to meet the needs of students by delivering a relevant, contemporary and engaging curriculum that builds on the educational goals of the Alice Springs (Mparntwe) Education Declaration. The Alice Springs (Mparntwe) Education Declaration identified three key areas that need to be addressed for the benefit of both individuals and Australia as a whole. In the Western Australian Curriculum these have become priorities that provide students with the tools and language to engage with and better understand their world at a range of levels. The priorities provide dimensions which will enrich the curriculum through development of considered and focused content that fits naturally within learning areas. They enable the delivery of learning area content at the same time as developing knowledge, understanding and skills relating to:
- Aboriginal and Torres Strait Islander histories and cultures
- Asia and Australia's engagement with Asia
- sustainability.
Cross-curriculum priorities are addressed through learning areas and are identified wherever they are developed or applied in content descriptions. They are also identified where they offer opportunities to add depth and richness to student learning in content elaborations. They will have a strong but varying presence depending on their relevance to the learning area.
Aboriginal and Torres Strait Islander histories and culture
Across the Western Australian Curriculum, the Aboriginal and Torres Strait Islander histories and cultures priority provides opportunities for all learners to deepen their knowledge of Australia by engaging with the world's oldest continuous living cultures. Students will understand that contemporary Aboriginal and Torres Strait Islander communities are strong, resilient, rich and diverse. The knowledge and understanding gained through this priority will enhance the ability of all young people to participate positively in the ongoing development of Australia.
The Western Australian Curriculum: Mathematics values Aboriginal and Torres Strait Islander histories and cultures. It provides opportunities for students to appreciate that Aboriginal and Torres Strait Islander societies have sophisticated applications of mathematical concepts.
Students will explore connections between representations of number and pattern and how they relate to aspects of Aboriginal and Torres Strait Islander cultures. They will investigate time, place, relationships and measurement concepts in Aboriginal and Torres Strait Islander contexts. Students will deepen their understanding of the lives of Aboriginal and Torres Strait Islander peoples through the application and evaluation of statistical data.
Asia and Australia's engagement with Asia
Across the Western Australian curriculum, this priority will ensure that students learn about and recognise the diversity within and between the countries of the Asia region. They will develop knowledge and understanding of Asian societies, cultures, beliefs and environments, and the connections between the peoples of Asia, Australia, and the rest of the world. Asia literacy provides students with the skills to communicate and engage with the peoples of Asia so they can effectively live, work and learn in the region.
In the Western Australian Curriculum: Mathematics, the priority of Asia and Australia's engagement with Asia provides rich and engaging contexts for developing students' mathematical knowledge, skills and understanding.
The Western Australian Curriculum: Mathematics provides opportunities for students to learn about the understandings and applications of Mathematics in Asia. Mathematicians from Asia continue to contribute to the ongoing development of Mathematics.
In this learning area, students develop mathematical understanding in fields such as number, patterns, measurement, symmetry and statistics by drawing on knowledge of and examples from the Asia region. These could include calculation, money, art, architecture, design and travel. Investigations involving data collection, representation and analysis can be used to examine issues pertinent to the Asia region.
Sustainability
Across the Western Australian Curriculum, sustainability will allow all young Australians to develop the knowledge, skills, values and world views necessary for them to act in ways that contribute to more sustainable patterns of living. It will enable individuals and communities to reflect on ways of interpreting and engaging with the world. The Sustainability priority is future-oriented, focusing on protecting environments and creating a more ecologically and socially just world through informed action. Actions that support more sustainable patterns of living require consideration of environmental, social, cultural and economic systems and their interdependence.
In the Western Australian Curriculum: Mathematics, the priority of sustainability provides rich, engaging and authentic contexts for developing students' abilities in number and algebra, measurement and geometry, and statistics and probability.
The Western Australian Curriculum: Mathematics provides opportunities for students to develop the proficiencies of problem solving and reasoning essential for the exploration of sustainability issues and their solutions. Mathematical understandings and skills are necessary to measure, monitor and quantify change in social, economic and ecological systems over time. Statistical analysis enables prediction of probable futures based on findings and helps inform decision making and actions that will lead to preferred futures.
In this learning area, students can observe, record and organise data collected from primary sources over time and analyse data relating to issues of sustainability from secondary sources. They can apply spatial reasoning, measurement, estimation, calculation and comparison to gauge local ecosystem health and can cost proposed actions for sustainability.
Links to the other learning areas
Learning in mathematics involves the use of knowledge and skills learnt in other areas, particularly in English, science and Humanities and Social Sciences.
The Australian National Numeracy Review Report (2008) identified numeracy as requiring an across-the-school commitment, including mathematical, strategic and contextual aspects. This across-the-school commitment can be managed by including specific references to other curriculum areas in the Mathematics curriculum, and the identification of key numeracy capacities in the descriptions of other curriculum areas being developed. For example, the following are some of the numeracy perspectives that could be relevant to English, Science and Humanities and Social Sciences.
English
One aspect of the link with English and literacy is that, along with other elements of study, numeracy can be understood and acquired only within the context of the social, cultural, political, economic and historical practices to which it is integral. Students need to be able to draw on quantitative and spatial information to derive meaning from certain types of texts encountered in the subject of English.
Science
Practical work and problem solving across all the sciences require the capacity to organise and represent data in a range of forms; plot, interpret and extrapolate graphs; estimate and solve ratio problems; use formulas flexibly in a range of situations; perform unit conversions; and use and interpret rates including concentrations, sampling, scientific notation, and significant figures.
Humanities and Social Sciences
Learning in Humanities and Social Sciences includes interpreting and representing large numbers and a range of data such as those associated with population statistics and growth, financial data, figures for exports and imports, immigration statistics, mortality rates, war enlistments and casualty figures; chance events, correlation and causation; imagining timelines and time frames to reconcile related events; and the perception and spatial visualisation required for geopolitical considerations, such as changes in borders of states and in ecology.
Implications for teaching, assessment and reporting
In mathematics, challenging problems can be posed using basic age-appropriate content. Accelerating students by using content beyond their year level may not be the best way to extend proficient mathematicians. Choosing engaging experiences as contexts for a variety of tasks assists in making mathematics inclusive, and these tasks can be effectively differentiated both for students experiencing difficulty and those who complete tasks easily. The proficiency strands apply expectations of the range and nature of how mathematical content is enacted, and can help focus teaching.
Teachers use the Western Australian Curriculum content and achievement standards first to identify current levels of learning and achievement and then to select the most appropriate content (possibly from across several year levels) to teach individual students and/or groups of students. This takes into account that in each class there may be students with a range of prior achievement (below, at, and above the year level expectations) and that teachers plan to build on current learning.
Teachers also use the achievement standards, at the end of a period of teaching, to make on-balance judgments about the quality of learning demonstrated by the students – that is whether they have achieved below, at, or above the standard. To make these judgments, teachers draw on assessment data that they have collected as evidence during the course of the teaching period. These judgments about the quality of learning are one source of feedback to students and their parents and inform formal reporting processes.
If a teacher judges that a student's achievement is below the expected standard, this suggests that the teaching programs and practice should be reviewed to better assist individual students in their learning in the future. It also suggests that additional support and targeted teaching will be needed to ensure that the student does not fall behind.
Assessment of the Western Australian Curriculum takes place in different levels and for different purposes, including:
- ongoing formative assessment within classrooms for the purposes of monitoring learning and providing feedback, to teachers to inform their teaching, and for students to inform their learning
- summative assessment for the purposes of twice-yearly reporting by schools to parents and carers on the progress and achievement of students
- annual testing of Years 3, 5, 7 and 9 students' levels of achievement in aspects of literacy and numeracy, conducted as part of the National Assessment Program – Literacy and Numeracy (NAPLAN)
- periodic sample testing of specific learning areas within the Western Australian Curriculum as part of the National Assessment Program (NAP).
Glossary
Mathematics v8.1
ABLEWA Stage A
The proficiency strands Understanding, Fluency, Problem Solving and Reasoning are an integral part of the mathematics content across the three content strands: Number and Algebra, Measurement and Geometry, Statistics and Probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics.
At this stage:
Understanding develops from becoming aware of their physical state and encountering, reacting and responding to the world around them and to some everyday events and routines
Fluency includes students learning to control their behaviour and internal state and developing a repertoire of reactions to everyday experiences and events
Problem Solving includes students attending to and exploring the world around them with as much independence as possible
Reasoning includes students coactively exploring and manipulating objects in their immediate environment and experiencing the language associated with maths activities.
Number and Algebra
Number and place value
Respond to objects being counted and distributed (ACMNA001a)
Respond to situations where counting is involved (ACMNA002a)
Respond to groups of personally relevant objects (ACMNA003a)
Respond to situations where the comparison of two collections or objects are involved (ACMNA289a)
Respond to the removal and addition of familiar items and objects in practical situations (ACMNA004a)
Patterns and algebra
Respond to the identification of objects (ACMNA005a)
Measurement and Geometry
Using units of measurement
Respond to objects based on length (ACMMG006a)
Respond to personally relevant everyday events (ACMMG007a)
Respond to personally relevant routine events (ACMMG008a)
Shape
Respond to familiar everyday shapes and objects (ACMMG009a)
Location and transformation
Respond to movement of an object (ACMMG010a)
Statistics and Probability
Data representation and interpretation
Respond to objects relevant to a given context (ACMSP011a)
Achievement standard
Number and Algebra
Students observe the use of number within their daily life. They begin to respond to numbers in everyday experiences. Students demonstrate awareness of counting by responding to number rhymes, songs, stories and finger games. They experience and respond to ‘one for you, one for me’, ‘gone’, ‘no more left’ and ‘give me more’. Students participate in making piles, groups or bundles of familiar everyday objects and respond to objects being put together and taken apart.
Measurement and Geometry
Students observe and explore objects within daily life. They react and respond to objects and experience measurement attributes in practical situations. Students explore objects of varying weights, lengths, capacities and materials. They show an awareness of time and daily routine by responding to a signal from the teacher, and items being brought out or removed. Students respond to a signal from a timer, used to indicate the end of an activity. Students explore and respond to objects of varying textures, colours, sizes and shapes. Students explore space by moving and changing position and location, and respond to changes in position.
Statistics and Probability
Students observe objects and events within their daily life. Students begin to display a similar and predictable reaction to regular events. They respond to major changes to regular games and activities associated with chance, surprise and predictability, such as hitting a switch to activate a toy.
ABLEWA Stage B
The proficiency strands Understanding, Fluency, Problem Solving and Reasoning are an integral part of the mathematics content across the three content strands: Number and Algebra, Measurement and Geometry, Statistics and Probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics.
At this stage:
Understanding develops through participating in a variety of everyday activities that involve objects, events and number
Fluency includes following regular routines, and matching objects using a repertoire of responses
Problem Solving includes students attending to, exploring and sorting objects in the world around them
Reasoning includes manipulating and playing with objects to develop links between their immediate environment, everyday language and mathematical activity.
Number and Algebra
Number and place value
Use number names ‘one’, ‘two’ and ‘three’ in sequence to count in everyday situations (ACMNA001b)
Correspond ‘one’ with a single object (ACMNA002b)
Explore the concept of ‘none’, ‘one’ and ‘more’ (ACMNA003b)
Make comparison between items using appropriate language such as ‘same’ or ‘different’ (ACMNA289b)
Participate in everyday situations involving ‘adding’ and ‘taking away’ (ACMNA004b)
Patterns and algebra
Participate in the comparing of objects, using language such as ‘same’ and ‘different’ (ACMNA005b)
Measurement and Geometry
Using units of measurement
Compare objects using direct comparison (ACMMG006b)
Recognise and participate in familiar events that happen on a daily basis (ACMMG007b)
Participate in regular daily events (ACMMG008b)
Shape
Identify when two shapes or objects are the same sort or not (ACMMG009b)
Location and transformation
Respond to a simple statement about location or direction (ACMMG010b)
Statistics and Probability
Data representation and interpretation
Participate in data collection (ACMSP011b)
Achievement standard
Number and Algebra
Students participate in everyday activities that involve numbers and counting, comparing groups of objects, and pattern activities. Students can rote count to three. Students identify ‘one’ and ‘lots’ of objects and show an understanding of ‘more’ in familiar situations. They manipulate objects and build a tall tower by using ‘more’ blocks and take blocks away from a tower to make the tower ‘less’ tall.
Measurement and Geometry
Students participate in everyday activities that explore measurement and use measurement attributes in practical situations. Students demonstrate beginning understanding of basic measurement concepts such as ‘long or short’, ‘heavy or light’,
They explore routine events and show an awareness of time and daily routines by responding to a routine signal from the teacher, such as, ‘It’s time to go outside and play’, ‘pack up’, or ‘unpack bag’
They demonstrate an awareness of object permanence by searching for objects that have been hidden and participate in class activities that explore three-dimensional objects. They can match identical familiar three-dimensional shapes that are ‘the same’. Students respond to specific instructions relating to manipulating the movement and location of self and objects.
Statistics and Probability They participate in class activities that explore object, events and displaying information. They develop an awareness of chance by playing with materials or objects that involve cause and effect (actions that will happen) and playing games where the outcome is unpredictable, for example, peekaboo. Students respond to a simple pictorial representation of their activities related to a short time-frame.
ABLEWA Stage C
The proficiency strands Understanding, Fluency, Problem Solving and Reasoning are an integral part of the mathematics content across the three content strands: Number and Algebra, Measurement and Geometry, Statistics and Probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics.
At this stage:
Understanding includes connecting names and quantities (of objects, events and numbers to five)
Fluency includes counting numbers in sequence, matching objects to replicate a pattern and predicting day and night events
Problem Solving includes matching groups and objects
Reasoningincludes manipulating and playing with objects to develop links between their immediate environment, everyday language, mathematical activity and concepts.
Number and Algebra
Number and place value
Use number names in sequence to count in everyday situations, initially from one to five (ACMNA001c)
Know and match number name, numerals and quantities to three (ACMNA002c)
Identify groups as being ‘one’, ‘more’ or ‘less’ (ACMNA003c)
Compare and order two collections according to their quantity (ACMNA289c)
Demonstrate in practical situations, ‘adding one more to’ and ‘taking one away from’ in everyday situations (ACMNA004c)
Patterns and algebra
Pair identical objects from a small collection. Recognise simple repeated patterns (ACMNA005c)
Measurement and Geometry
Using units of measurement
Compare two objects based on measurement attributes of length (ACMMG006c)
Identify familiar events that occur at different stages of a day (morning, afternoon, evening, night) (ACMMG007c)
Identify the familiar events within the day using a visual schedule (ACMMG008c)
Shape
Match familiar two dimensional shapes and three dimensional objects (ACMMG009c)
Location and transformation
Locate familiar three-dimensional objects in the classroom when they are named (ACMMG010c)
Statistics and Probability
Data representation and interpretation
Identify data relevant to a given context (ACMSP011c)
Achievement standard
Number and Algebra
Students connect number names and numerals with sets of up to five elements. They match individual objects with counting sequences up to and back from five. Students use concrete materials to solve problems that involve comparing, combining and separating sets, for example “How might I make this group more than the other group?” Students make ‘groups’, ‘lots’ and groups of ‘one’ and can indicate which collection has ‘more’ than the other. They can distribute objects to each person in a group until there are no objects left. Students order the first three elements of a set. Students can match one attribute of familiar objects, for example, colour, size or shape.
Measurement and Geometry
Students explore measurement attributes in practical situations and use words to describe the characteristics of familiar objects such as full, empty, long, short, light and heavy. Students solve simple mathematical problems associated with longer and shorter lengths, for example, ‘How can I make this stick shorter?’ They explore events and identify day and night events. They can identify events that may or may not happen today. Students respond to a simple pictorial representation of activities related to their whole day. They match objects that are the same and sort familiar objects, and an understanding of the concept of ‘inside and outside’ by following instructions. They demonstrate an understanding of location and spatial awareness by following simple instructions related to simple spatial concepts, such as ‘under’, ‘on’, ‘beside’.
Statistics and Probability Students participate in and contribute to the development of picture schedules, timetables and pictorial lists associated with familiar activities, such as listing the ingredients needed for a cooking session. They demonstrate an understanding of the concept of chance by participating in games of chance, and identifying events that may or may not happen today.
ABLEWA Stage D
The proficiency strands Understanding, Fluency, Problem Solving and Reasoning are an integral part of the mathematics content across the three content strands: Number and Algebra, Measurement and Geometry, Statistics and Probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics.
At this stage:
Understanding includes connecting names, numerals and quantities of objects, events and numbers to 10
Fluency includes counting number in sequence, continuing patterns, comparing objects, recognising events in the day
Problem Solving includes manipulating, comparing and sorting objects, such as which group (out of three) has more or less Reasoning includes manipulating and playing with objects to develop links between their immediate environment, everyday language and mathematical activity.
Number and Algebra
Number and place value
Use a number names in sequence to count in everyday situations, initially from one to ten (ACMNA001d)
Recognise number name, numerals and quantities, initially up to five and beyond (ACMNA002d)
Subitise regular arrangements of objects and arrays up to five (ACMNA003d)
Compare, order and make comparisons between two collections, according to their quantity, using numbers initially to five (ACMNA289d)
Model practical situations involving ‘adding to’ or ‘taking away’ with collections of up to five objects (ACMNA004d)
Patterns and algebra
Sort like objects based on a given classification. Identify and continue a simple repeated pattern with its next element (ACMNA005d)
Measurement and Geometry
Using units of measurement
Respond to contexts involving ‘heavier/lighter’ than and ‘holds more/less’ than (ACMMG006d)
Identify and sequence regular events that occur during the school day and comment on their duration (short/long) (ACMMG007d)
Identify the days of the week in sequence (ACMMG008d)
Shape
Use direct comparison to sort three dimensional objects and two dimensional shapes (ACMMG009d)
Location and transformation
Follow simple directional words, to locate or move an object ‘on’, ‘in’ or ‘under’ (ACMMG010d)
Statistics and Probability
Data representation and interpretation
Answer simple yes/no questions about data that has been gathered in a given context (ACMSP011d)
Achievement standard
Number and Algebra
Students connect number names and numerals with sets of up to 10 elements. They match individual objects with counting sequences up to and back from 10. They recognise and point to numerals in and around the classroom, for example, numbers on a clock face. Students use concrete materials to solve problems that involve comparing, combining and separating sets. They can indicate when groups of less than 10 objects are the same or different in number and that two collections have the ‘same’ quantity by matching items one to one. They can find the first and last object in a sequence and place objects into sets to make ‘more’ and take objects from a group to make ‘less’. Students order the first five elements of a set. They sort objects and shapes based on a given attribute and create simple repeating patterns of two elements or more by copying a pattern.
Measurement and Geometry
Students explore measurement attributes in practical situations and identify and describe the basic characteristics of a range of objects, for example, heights of students, cup measures in cooking. They can identify regular events within the school week. They can follow a class pictorial schedule and mark off each passing day on a calendar. Students demonstrate an understanding of two- and three-dimensional shapes by matching basic geometric objects to pictures of that object, identifying basic three-dimensional shapes in the classroom and sorting shapes into like groups. Students show an understanding of ‘location’ and spatial concepts by responding to instructions to position items.
Statistics and Probability
They explore events and follow a simple picture schedule, and use these to answer simple ‘yes’ or ‘no’ questions. They play a variety of chance games such as bingo or snakes and ladders and demonstrate an understanding that they will not always win.
Pre-primary year Syllabus
Year Level Description
The proficiency strands understanding, fluency, problem-solving and reasoning are an integral part of mathematics content across the three content strands: number and algebra, measurement and geometry, and statistics and probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics. The achievement standards reflect the content and encompass the proficiencies.
At this year level:
- understanding includes connecting names, numerals and quantities
- fluency includes readily counting numbers in sequences, continuing patterns and comparing the lengths of objects
- problem-solving includes using materials to model authentic problems, sorting objects, using familiar counting sequences to solve unfamiliar problems and discussing the reasonableness of the answer
- reasoning includes explaining comparisons of quantities, creating patterns and explaining processes for indirect comparison of length
Number and algebra
Number and place value
Establish understanding of the language and processes of counting by naming numbers in sequences, initially to and from 20, moving from any starting point (ACMNA001)
Connect number names, numerals and quantities, including zero, initially up to 10 and then beyond (ACMNA002)
Subitise small collections of objects (ACMNA003)
Compare, order and make correspondences between collections, initially to 20, and explain reasoning (ACMNA289)
Represent practical situations to model addition and sharing (ACMNA004)
Patterns and algebra
Sort and classify familiar objects and explain the basis for these classifications. Copy, continue and create patterns with objects and drawings (ACMNA005)
Measurement and Geometry
Using units of measurement
Use direct and indirect comparisons to decide which is longer, heavier or holds more, and explain reasoning in everyday language (ACMMG006)
Compare and order duration of events using everyday language of time (ACMMG007)
Connect days of the week to familiar events and actions (ACMMG008)
Shape
Sort, describe and name familiar two-dimensional shapes and three-dimensional objects in the environment (ACMMG009)
Location and transformation
Describe position and movement (ACMMG010)
Statistics and Probability
Data representation and interpretation
Answer yes/no questions to collect information and make simple inferences (ACMSP011)
Pre-primary Achievement Standard
Number and Algebra
At Standard, students count to and from 20 and order small collections. They make connections between number names, numerals and quantities up to 10.
Measurement and Geometry
Students compare objects using mass, length and capacity. They explain the order and duration of events. Students connect events and the days of the week. They group objects based on common characteristics and sort shapes and objects. Students use appropriate language to describe location.
Statistics and Probability
Students answer simple questions to collect information and make simple inferences.
Year 1 Syllabus
Year Level Description
The proficiency strands understanding, fluency, problem-solving and reasoning are an integral part of mathematics content across the three content strands: number and algebra, measurement and geometry, and statistics and probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics. The achievement standards reflect the content and encompass the proficiencies.
At this year level:
- understanding includes connecting names, numerals and quantities, and partitioning numbers in various ways
- fluency includes readily counting number in sequences forwards and backwards, locating numbers on a line and naming the days of the week
- problem-solving includes using materials to model authentic problems, giving and receiving directions to unfamiliar places, using familiar counting sequences to solve unfamiliar problems and discussing the reasonableness of the answer
- reasoning includes explaining direct and indirect comparisons of length using uniform informal units, justifying representations of data and explaining patterns that have been created.
Number and Algebra
Number and place value
Develop confidence with number sequences to and from 100 by ones from any starting point. Skip count by twos, fives and tens starting from zero (ACMNA012)
Recognise, model, read, write and order numbers to at least 100. Locate these numbers on a number line (ACMNA013)
Count collections to 100 by partitioning numbers using place value (ACMNA014)
Represent and solve simple addition and subtraction problems using a range of strategies including counting on, partitioning and rearranging parts (ACMNA015)
Fractions and decimals
Recognise and describe one-half as one of two equal parts of a whole (ACMNA016)
Money and financial mathematics
Recognise, describe and order Australian coins according to their value (ACMNA017)
Patterns and algebra
Investigate and describe number patterns formed by skip-counting and patterns with objects (ACMNA018)
Measurement and Geometry
Using units of measurement
Measure and compare the lengths and capacities of pairs of objects using uniform informal units (ACMMG019)
Tell time to the half-hour (ACMMG020)
Describe duration using months, weeks, days and hours (ACMMG021)
Shape
Recognise and classify familiar two-dimensional shapes and three-dimensional objects using obvious features (ACMMG022)
Location and transformation
Give and follow directions to familiar locations (ACMMG023)
Statistics and Probability
Chance
Identify outcomes of familiar events involving chance and describe them using everyday language such as ‘will happen’, ‘won’t happen’ or ‘might happen’ (ACMSP024)
Data representation and interpretation
Choose simple questions and gather responses and make simple inferences (ACMSP262)
Represent data with objects and drawings where one object or drawing represents one data value. Describe the displays (ACMSP263)
Year 1 Achievement Standard
Number and Algebra
At Standard, students count to and from 100 and locate numbers on a number line. They partition numbers using place value. Students carry out simple additions and subtractions using counting strategies. They identify representations of one half. Students recognise Australian coins according to their value. They continue simple patterns involving numbers and objects. Students describe number sequences resulting from skip counting by 2s, 5s and 10s.
Measurement and Geometry
Students order objects based on lengths and capacities using informal units. They tell time to the half hour and explain time durations. Students describe two-dimensional shapes and three-dimensional objects. They use the language of direction to move from place to place.
Statistics and Probability
Students classify outcomes of simple familiar events. They collect data by asking questions, draw simple data displays and make simple inferences. Students describe data displays.
Year 2 Syllabus
Year Level Description
The proficiency strands understanding, fluency, problem-solving and reasoning are an integral part of mathematics content across the three content strands: number and algebra, measurement and geometry, and statistics and probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics. The achievement standards reflect the content and encompass the proficiencies.
At this year level:
- understanding includes connecting number calculations with counting sequences, partitioning and combining numbers flexibly and identifying and describing the relationship between addition and subtraction and between multiplication and division
- fluency includes readily counting numbers in sequences, using informal units iteratively to compare measurements, using the language of chance to describe outcomes of familiar chance events and describing and comparing time durations
- problem-solving includes formulating problems from authentic situations, making models and using number sentences that represent problem situations, and matching transformations with their original shape
- reasoning includes using known facts to derive strategies for unfamiliar calculations, comparing and contrasting related models of operations and creating and interpreting simple representations of data.
Number and Algebra
Number and place value
Investigate number sequences, initially those increasing and decreasing by twos, threes, fives and tens from any starting point, then moving to other sequences (ACMNA026)
Recognise, model, represent and order numbers to at least 1000 (ACMNA027)
Group, partition and rearrange collections up to 1000 in hundreds, tens and ones to facilitate more efficient counting (ACMNA028)
Explore the connection between addition and subtraction (ACMNA029)
Solve simple addition and subtraction problems using a range of efficient mental and written strategies (ACMNA030)
Recognise and represent multiplication as repeated addition, groups and arrays (ACMNA031)
Recognise and represent division as grouping into equal sets and solve simple problems using these representations (ACMNA032)
Fractions and decimals
Recognise and interpret common uses of halves, quarters and eighths of shapes and collections (ACMNA033)
Money and financial mathematics
Count and order small collections of Australian coins and notes according to their value (ACMNA034)
Patterns and algebra
Describe patterns with numbers and identify missing elements (ACMNA035)
Solve problems by using number sentences for addition or subtraction (ACMNA036)
Measurement and Geometry
Using units of measurement
Compare and order several shapes and objects based on length, area, volume and capacity using appropriate uniform informal units (ACMMG037)
Compare masses of objects using balance scales (ACMMG038)
Tell time to the quarter-hour, using the language of 'past' and 'to' (ACMMG039)
Name and order months and seasons (ACMMG040)
Use a calendar to identify the date and determine the number of days in each month (ACMMG041)
Shape
Describe and draw two-dimensional shapes, with and without digital technologies (ACMMG042)
Describe the features of three-dimensional objects (ACMMG043)
Location and transformation
Interpret simple maps of familiar locations and identify the relative positions of key features (ACMMG044)
Investigate the effect of one-step slides and flips with and without digital technologies (ACMMG045)
Identify and describe half and quarter turns (ACMMG046)
Statistics and Probability
Chance
Identify practical activities and everyday events that involve chance. Describe outcomes as ‘likely’ or ‘unlikely’ and identify some events as ‘certain’ or ‘impossible’ (ACMSP047)
Data representation and interpretation
Identify a question of interest based on one categorical variable. Gather data relevant to the question (ACMSP048)
Collect, check and classify data (ACMSP049)
Create displays of data using lists, table and picture graphs and interpret them (ACMSP050)
Year 2 Achievement Standard
Number and Algebra
At Standard, students count to and from 1000. They perform simple addition and subtraction calculations using a range of strategies. Students represent multiplication and division by grouping into sets. They divide collections and shapes into halves, quarters and eighths. Students associate collections of Australian coins with their value. They recognise increasing and decreasing number sequences involving 2s, 3s and 5s. Students identify the missing element in a number sequence.
Measurement and Geometry
Students order shapes and objects using informal units. They tell time to the quarter hour and use a calendar to identify the date and the months included in seasons. Students recognise the features of three-dimensional objects. They draw two-dimensional shapes. Students interpret simple maps of familiar locations. They explain the effects of one-step transformations.
Statistics and Probability
Students describe outcomes for everyday events. They collect, organise and represent data to make simple inferences. Students make sense of collected information.
Year 3 Syllabus
Year Level Description
The proficiency strands understanding, fluency, problem-solving and reasoning are an integral part of mathematics content across the three content strands: number and algebra, measurement and geometry, and statistics and probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics. The achievement standards reflect the content and encompass the proficiencies.
At this year level:
- understanding includes connecting number representations with number sequences, partitioning and combining numbers flexibly, representing unit fractions, using appropriate language to communicate times, and identifying environmental symmetry
- fluency includes recalling multiplication facts, using familiar metric units to order and compare objects, identifying and describing outcomes of chance experiments, interpreting maps and communicating positions
- problem-solving includes formulating and modelling authentic situations involving planning methods of data collection and representation, making models of three-dimensional objects and using number properties to continue number patterns
- reasoning includes using generalising from number properties and results of calculations, comparing angles and creating and interpreting variations in the results of data collections and data displays.
Number and Algebra
Number and place value
Investigate the conditions required for a number to be odd or even and identify odd and even numbers (ACMNA051)
Recognise, model, represent and order numbers to at least 10 000 (ACMNA052)
Apply place value to partition, rearrange and regroup numbers to at least 10 000 to assist calculations and solve problems (ACMNA053)
Recognise and explain the connection between addition and subtraction (ACMNA054)
Recall addition facts for single-digit numbers and related subtraction facts to develop increasingly efficient mental strategies for computation (ACMNA055)
Recall multiplication facts of two, three, five and ten and related division facts (ACMNA056)
Represent and solve problems involving multiplication using efficient mental and written strategies and appropriate digital technologies (ACMNA057)
Fractions and decimals
Model and represent unit fractions including 1/2, 1/4, 1/3, 1/5 and their multiples to a complete whole (ACMNA058)
Money and financial mathematics
Represent money values in multiple ways and count the change required for simple transactions to the nearest five cents (ACMNA059)
Patterns and algebra
Describe, continue, and create number patterns resulting from performing addition or subtraction (ACMNA060)
Measurement and Geometry
Using units of measurement
Measure, order and compare objects using familiar metric units of length, mass and capacity (ACMMG061)
Tell time to the minute and investigate the relationship between units of time (ACMMG062)
Shape
Make models of three-dimensional objects and describe key features (ACMMG063)
Location and transformation
Create and interpret simple grid maps to show position and pathways (ACMMG065)
Identify symmetry in the environment (ACMMG066)
Geometric reasoning
Identify angles as measures of turn and compare angle sizes in everyday situations (ACMMG064)
Statistics and Probability
Chance
Conduct chance experiments, identify and describe possible outcomes and recognise variation in results (ACMSP067)
Data representation and interpretation
Identify questions or issues for categorical variables. Identify data sources and plan methods of data collection and recording (ACMSP068)
Collect data, organise into categories and create displays using lists, tables, picture graphs and simple column graphs, with and without the use of digital technologies (ACMSP069)
Interpret and compare data displays (ACMSP070)
Year 3 Achievement Standard
Number and Algebra
At Standard, students count to and from 10 000. They classify numbers as either odd or even. Students recall addition and multiplication facts for single-digit numbers. They recognise the connection between addition and subtraction and solve problems using efficient strategies for multiplication. Students model and represent unit fractions. They represent money values in various ways. Students correctly count out change from financial transactions. They continue number patterns involving addition and subtraction.
Measurement and Geometry
Students use metric units for length, mass and capacity. They tell time to the nearest minute. Students make models of three-dimensional objects. They match positions on maps with given information. Students identify symmetry in the environment. They recognise angles in real situations.
Statistics and Probability
Students conduct chance experiments and list possible outcomes. They conduct simple data investigations for categorical variables. Students interpret and compare data displays.
Year 4 Syllabus
Year Level Description
The proficiency strands understanding, fluency, problem-solving and reasoning are an integral part of mathematics content across the three content strands: number and algebra, measurement and geometry, and statistics and probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics. The achievement standards reflect the content and encompass the proficiencies.
At this year level:
- understanding includes making connections between representations of numbers, partitioning and combining numbers flexibly, extending place value to decimals, using appropriate language to communicate times and describing properties of symmetrical shapes
- fluency includes recalling multiplication tables, communicating sequences of simple fractions, using instruments to measure accurately, creating patterns with shapes and their transformations and collecting and recording data
- problem-solving includes formulating, modelling and recording authentic situations involving operations, comparing large numbers with each other, comparing time durations and using properties of numbers to continue patterns
- reasoning includes using generalising from number properties and results of calculations, deriving strategies for unfamiliar multiplication and division tasks, comparing angles, communicating information using graphical displays and evaluating the appropriateness of different displays.
Number and Algebra
Number and place value
Investigate and use the properties of odd and even numbers (ACMNA071)
Recognise, represent and order numbers to at least tens of thousands (ACMNA072)
Apply place value to partition, rearrange and regroup numbers to at least tens of thousands to assist calculations and solve problems (ACMNA073)
Investigate number sequences involving multiples of 3, 4, 6, 7, 8, and 9 (ACMNA074)
Recall multiplication facts up to 10 × 10 and related division facts (ACMNA075)
Develop efficient mental and written strategies and use appropriate digital technologies for multiplication and for division where there is no remainder (ACMNA076)
Fractions and decimals
Investigate equivalent fractions used in contexts (ACMNA077)
Count by quarters halves and thirds, including with mixed numerals. Locate and represent these fractions on a number line (ACMNA078)
Recognise that the place value system can be extended to tenths and hundredths. Make connections between fractions and decimal notation (ACMNA079)
Money and financial mathematics
Solve problems involving purchases and the calculation of change to the nearest five cents with and without digital technologies (ACMNA080)
Patterns and algebra
Explore and describe number patterns resulting from performing multiplication (ACMNA081)
Solve word problems by using number sentences involving multiplication or division where there is no remainder (ACMNA082)
Find unknown quantities in number sentences involving addition and subtraction and identify equivalent number sentences involving addition and subtraction (ACMNA083)
Measurement and Geometry
Using units of measurement
Use scaled instruments to measure and compare lengths, masses, capacities and temperatures (ACMMG084)
Compare objects using familiar metric units of area and volume (ACMMG290)
Convert between units of time (ACMMG085)
Use ‘am’ and ‘pm’ notation and solve simple time problems (ACMMG086)
Shape
Compare the areas of regular and irregular shapes by informal means (ACMMG087)
Compare and describe two dimensional shapes that result from combining and splitting common shapes, with and without the use of digital technologies (ACMMG088)
Location and transformation
Use simple scales, legends and directions to interpret information contained in basic maps (ACMMG090)
Create symmetrical patterns, pictures and shapes with and without digital technologies (ACMMG091)
Geometric reasoning
Compare angles and classify them as equal to, greater than, or less than, a right angle (ACMMG089)
Statistics and Probability
Chance
Describe possible everyday events and order their chances of occurring (ACMSP092)
Identify everyday events where one cannot happen if the other happens (ACMSP093)
Identify events where the chance of one will not be affected by the occurrence of the other (ACMSP094)
Data representation and interpretation
Select and trial methods for data collection, including survey questions and recording sheets (ACMSP095)
Construct suitable data displays, with and without the use of digital technologies, from given or collected data. Include tables, column graphs and picture graphs where one picture can represent many data values (ACMSP096)
Evaluate the effectiveness of different displays in illustrating data features including variability (ACMSP097)
Year 4 Achievement Standard
Number and Algebra
At Standard, students use the properties of odd and even numbers. They recall multiplication facts to 10 x 10 and related division facts. Students continue number sequences involving multiples of single-digit numbers. They choose appropriate strategies for calculations involving multiplication and division. Students locate familiar fractions on a number line. They recognise common equivalent fractions in familiar contexts and make connections between fraction and decimal notations up to two decimal places. Students solve simple purchasing problems. They describe number patterns resulting from multiplication. Students identify and explain strategies for finding unknown quantities in number sentences.
Measurement and Geometry
Students use scaled instruments to measure temperatures, lengths, shapes and objects. They compare areas of regular and irregular shapes using informal units. Students solve problems involving time duration. They convert between units of time. Students interpret information contained in maps. They create symmetrical shapes and patterns. They classify angles in relation to a right angle.
Statistics and Probability
Students list the probabilities of everyday events. They identify dependent and independent events. Students describe different methods for data collection and representation and evaluate their effectiveness. They construct data displays from given or collected data.
Year 5 Syllabus
Year Level Description
The proficiency strands understanding, fluency, problem-solving and reasoning are an integral part of mathematics content across the three content strands: number and algebra, measurement and geometry, and statistics and probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics. The achievement standards reflect the content and encompass the proficiencies.
At this year level:
- understanding includes making connections between representations of numbers, using fractions to represent probabilities, comparing and ordering fractions and decimals and representing them in various ways, describing transformations and identifying line and rotational symmetry
- fluency includes choosing appropriate units of measurement for calculation of perimeter and area, using estimation to check the reasonableness of answers to calculations and using instruments to measure angles
- problem-solving includes formulating and solving authentic problems using whole numbers and measurements and creating financial plans
- reasoning includes investigating strategies to perform calculations efficiently, continuing patterns involving fractions and decimals, interpreting results of chance experiments, posing appropriate questions for data investigations and interpreting data sets.
Number and Algebra
Number and place value
Identify and describe factors and multiples of whole numbers and use them to solve problems (ACMNA098)
Use estimation and rounding to check the reasonableness of answers to calculations (ACMNA099)
Solve problems involving multiplication of large numbers by one- or two-digit numbers using efficient mental, written strategies and appropriate digital technologies (ACMNA100)
Solve problems involving division by a one digit number, including those that result in a remainder (ACMNA101)
Use efficient mental and written strategies and apply appropriate digital technologies to solve problems (ACMNA291)
Fractions and decimals
Compare and order common unit fractions and locate and represent them on a number line (ACMNA102)
Investigate strategies to solve problems involving addition and subtraction of fractions with the same denominator (ACMNA103)
Recognise that the place value system can be extended beyond hundredths (ACMNA104)
Compare, order and represent decimals (ACMNA105)
Money and financial mathematics
Create simple financial plans (ACMNA106)
Patterns and algebra
Describe, continue and create patterns with fractions, decimals and whole numbers resulting from addition and subtraction (ACMNA107)
Find unknown quantities in number sentences involving multiplication and division and identify equivalent number sentences involving multiplication and division (ACMNA121)
Measurement and Geometry
Using units of measurement
Choose appropriate units of measurement for length, area, volume, capacity and mass (ACMMG108)
Calculate perimeter and area of rectangles using familiar metric units (ACMMG109)
Compare 12- and 24-hour time systems and convert between them (ACMMG110)
Shape
Connect three-dimensional objects with their nets and other two-dimensional representations (ACMMG111)
Location and transformation
Use a grid reference system to describe locations. Describe routes using landmarks and directional language (ACMMG113)
Describe translations, reflections and rotations of two-dimensional shapes. Identify line and rotational symmetries (ACMMG114)
Apply the enlargement transformation to familiar two dimensional shapes and explore the properties of the resulting image compared with the original (ACMMG115)
Geometric reasoning
Estimate, measure and compare angles using degrees. Construct angles using a protractor (ACMMG112)
Statistics and Probability
Chance
List outcomes of chance experiments involving equally likely outcomes and represent probabilities of those outcomes using fractions (ACMSP116)
Recognise that probabilities range from 0 to 1 (ACMSP117)
Data representation and interpretation
Pose questions and collect categorical or numerical data by observation or survey (ACMSP118)
Construct displays, including column graphs, dot plots and tables, appropriate for data type, with and without the use of digital technologies (ACMSP119)
Describe and interpret different data sets in context (ACMSP120)
Year 5 Achievement Standard
Number and Algebra
At Standard, students identify and describe factors and multiples. They solve simple problems involving the four operations using a range of strategies. Students check the reasonableness of answers using estimation and rounding. They order decimals and unit fractions and locate them on number lines. Students add and subtract fractions with the same denominator. They explain plans for simple budgets. Students continue patterns by adding and subtracting fractions and decimals. They identify and explain strategies for finding unknown quantities in number sentences involving the four operations.
Measurement and Geometry
Students use appropriate units of measurement for length, area, volume, capacity and mass, and calculate perimeter and area of rectangles. They convert between 12 and 24 hour time. Students connect three-dimensional objects with their two-dimensional representations. They describe transformations of two-dimensional shapes and identify line and rotational symmetry. Students use a grid reference system to locate landmarks. They measure and construct different angles.
Statistics and Probability
Students interpret different data sets. They list outcomes of chance experiments with equally likely outcomes and assign probabilities between 0 and 1. Students pose questions to gather data, and construct data displays appropriate for the data.
Year 6 Syllabus
Year Level Description
The proficiency strands understanding, fluency, problem-solving and reasoning are an integral part of mathematics content across the three content strands: number and algebra, measurement and geometry, and statistics and probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics. The achievement standards reflect the content and encompass the proficiencies.
At this year level:
- understanding includes describing properties of different sets of numbers, using fractions and decimals to describe probabilities, representing fractions and decimals in various ways and describing connections between them, and making reasonable estimations
- fluency includes representing integers on a number line, calculating simple percentages, using brackets appropriately, converting between fractions and decimals, using operations with fractions, decimals and percentages, measuring using metric units and interpreting timetables
- problem-solving includes formulating and solving authentic problems using fractions, decimals, percentages and measurements, interpreting secondary data displays and finding the size of unknown angles
- reasoning includes explaining mental strategies for performing calculations, describing results for continuing number sequences, explaining the transformation of one shape into another and explaining why the actual results of chance experiments may differ from expected results.
Number and Algebra
Number and place value
Identify and describe properties of prime, composite, square and triangular numbers (ACMNA122)
Select and apply efficient mental and written strategies and appropriate digital technologies to solve problems involving all four operations with whole numbers (ACMNA123)
Investigate everyday situations that use integers. Locate and represent these numbers on a number line (ACMNA124)
Fractions and decimals
Compare fractions with related denominators and locate and represent them on a number line (ACMNA125)
Solve problems involving addition and subtraction of fractions with the same or related denominators (ACMNA126)
Find a simple fraction of a quantity where the result is a whole number, with and without digital technologies (ACMNA127)
Add and subtract decimals, with and without digital technologies, and use estimation and rounding to check the reasonableness of answers (ACMNA128)
Multiply decimals by whole numbers and perform divisions by non-zero whole numbers where the results are terminating decimals, with and without digital technologies (ACMNA129)
Multiply and divide decimals by powers of 10 (ACMNA130)
Make connections between equivalent fractions, decimals and percentages (ACMNA131)
Money and financial mathematics
Investigate and calculate percentage discounts of 10%, 25% and 50% on sale items, with and without digital technologies (ACMNA132)
Patterns and algebra
Continue and create sequences involving whole numbers, fractions and decimals. Describe the rule used to create the sequence (ACMNA133)
Explore the use of brackets and order of operations to write number sentences (ACMNA134)
Measurement and Geometry
Using units of measurement
Connect decimal representations to the metric system (ACMMG135)
Convert between common metric units of length, mass and capacity (ACMMG136)
Solve problems involving the comparison of lengths and areas using appropriate units (ACMMG137)
Connect volume and capacity and their units of measurement (ACMMG138)
Interpret and use timetables (ACMMG139)
Shape
Construct simple prisms and pyramids (ACMMG140)
Location and transformation
Investigate combinations of translations, reflections and rotations, with and without the use of digital technologies (ACMMG142)
Introduce the Cartesian coordinate system using all four quadrants (ACMMG143)
Geometric reasoning
Investigate, with and without digital technologies, angles on a straight line, angles at a point and vertically opposite angles. Use results to find unknown angles (ACMMG141)
Statistics and Probability
Chance
Describe probabilities using fractions, decimals and percentages (ACMSP144)
Conduct chance experiments with both small and large numbers of trials using appropriate digital technologies (ACMSP145)
Compare observed frequencies across experiments with expected frequencies (ACMSP146)
Data representation and interpretation
Interpret and compare a range of data displays, including side-by-side column graphs for two categorical variables (ACMSP147)
Interpret secondary data presented in digital media and elsewhere (ACMSP148)
Year 6 Achievement Standard
Number and Algebra
At Standard, students recognise the properties of prime, composite, square and triangular numbers. They describe the use of integers in everyday contexts. Students solve problems involving all four operations with whole numbers. They locate fractions and integers on a number line. Students solve problems involving the addition and subtraction of related fractions. They calculate a simple fraction of a quantity. Students connect fractions, decimals and percentages as different representations of the same number. They make connections between the powers of 10 and the multiplication and division of decimals. Students add, subtract and multiply decimals and divide decimals where the result is rational. They calculate common percentage discounts on sale items. Students describe rules used in sequences involving whole numbers, fractions and decimals. They write correct number sentences using brackets and order of operations.
Measurement and Geometry
Students connect decimal representations to the metric system and choose appropriate units of measurement to perform a calculation. They make connections between capacity and volume. Students solve problems involving length and area. They interpret timetables. Students construct simple prisms and pyramids. They describe combinations of transformations. Students solve problems using the properties of angles. They locate an ordered pair in any one of the four quadrants on the Cartesian plane.
Statistics and Probability
Students compare observed and expected frequencies. They describe probabilities using simple fractions, decimals and percentages. Students interpret and compare a variety of data displays including those displays for two categorical variables. They interpret secondary data displayed in the media.
Year 7 Syllabus
Year Level Description
The proficiency strands understanding, fluency, problem-solving and reasoning are an integral part of mathematics content across the three content strands: number and algebra, measurement and geometry, and statistics and probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics. The achievement standards reflect the content and encompass the proficiencies.
At this year level:
- understanding includes describing patterns in uses of indices with whole numbers, recognising equivalences between fractions, decimals, percentages and ratios, plotting points on the Cartesian plane, identifying angles formed by a transversal crossing a pair of lines, and connecting the laws and properties of numbers to algebraic terms and expressions
- fluency includes calculating accurately with integers, representing fractions and decimals in various ways, investigating best buys, finding measures of central tendency and calculating areas of shapes and volumes of prisms
- problem-solving includes formulating and solving authentic problems using numbers and measurements, working with transformations and identifying symmetry, calculating angles and interpreting sets of data collected through chance experiments
- reasoning includes applying the number laws to calculations, applying known geometric facts to draw conclusions about shapes, applying an understanding of ratio and interpreting data displays.
Number and Algebra
Number and place value
Investigate index notation and represent whole numbers as products of powers of prime numbers (ACMNA149)
Investigate and use square roots of perfect square numbers (ACMNA150)
Apply the associative, commutative and distributive laws to aid mental and written computation (ACMNA151)
Compare, order, add and subtract integers (ACMNA280)
Real numbers
Compare fractions using equivalence. Locate and represent positive and negative fractions and mixed numbers on a number line (ACMNA152)
Solve problems involving addition and subtraction of fractions, including those with unrelated denominators (ACMNA153)
Multiply and divide fractions and decimals using efficient written strategies and digital technologies (ACMNA154)
Express one quantity as a fraction of another, with and without the use of digital technologies (ACMNA155)
Round decimals to a specified number of decimal places (ACMNA156)
Connect fractions, decimals and percentages and carry out simple conversions (ACMNA157)
Find percentages of quantities and express one quantity as a percentage of another, with and without digital technologies (ACMNA158)
Recognise and solve problems involving simple ratios (ACMNA173)
Money and financial mathematics
Investigate and calculate 'best buys', with and without digital technologies (ACMNA174)
Patterns and algebra
Introduce the concept of variables as a way of representing numbers using letters (ACMNA175)
Create algebraic expressions and evaluate them by substituting a given value for each variable (ACMNA176)
Extend and apply the laws and properties of arithmetic to algebraic terms and expressions (ACMNA177)
Linear and non-linear relationships
Given coordinates, plot points on the Cartesian plane, and find coordinates for a given point (ACMNA178)
Solve simple linear equations (ACMNA179)
Investigate, interpret and analyse graphs from authentic data (ACMNA180)
Measurement and Geometry
Using units of measurement
Establish the formulas for areas of rectangles, triangles and parallelograms, and use these in problem-solving (ACMMG159)
Calculate volumes of rectangular prisms (ACMMG160)
Shape
Draw different views of prisms and solids formed from combinations of prisms (ACMMG161)
Location and transformation
Describe translations, reflections in an axis and rotations of multiples of 90° on the Cartesian plane using coordinates. Identify line and rotational symmetries (ACMMG181)
Geometric reasoning
Identify corresponding, alternate and co-interior angles when two straight lines are crossed by a transversal (ACMMG163)
Investigate conditions for two lines to be parallel and solve simple numerical problems using reasoning (ACMMG164)
Demonstrate that the angle sum of a triangle is 180° and use this to find the angle sum of a quadrilateral (ACMMG166)
Classify triangles according to their side and angle properties and describe quadrilaterals (ACMMG165)
Statistics and Probability
Chance
Construct sample spaces for single-step experiments with equally likely outcomes (ACMSP167)
Assign probabilities to the outcomes of events and determine probabilities for events (ACMSP168)
Data representation and interpretation
Identify and investigate issues involving numerical data collected from primary and secondary sources (ACMSP169)
Construct and compare a range of data displays including stem-and-leaf plots and dot plots (ACMSP170)
Calculate mean, median, mode and range for sets of data. Interpret these statistics in the context of data (ACMSP171)
Describe and interpret data displays using median, mean and range (ACMSP172)
Year 7 Achievement Standard
Number and Algebra
At Standard, students solve problems involving the comparison, addition and subtraction of integers. They make the connections between whole numbers and index notation and the relationship between perfect squares and square roots. Students use fractions, decimals and percentages, and their equivalences. They express one quantity as a fraction or percentage of another. Students solve problems involving percentages and all four operations with fractions and decimals. They compare the cost of items to make financial decisions. Students represent numbers using variables. They connect the laws and properties for numbers to algebra. Students assign ordered pairs to given points on the Cartesian plane. They interpret simple linear representations and model authentic information. Students solve simple linear equations and evaluate algebraic expressions after numerical substitution.
Measurement and Geometry
Students describe different views of three-dimensional objects. They represent transformations in the Cartesian plane. Students solve simple numerical problems involving angles formed by a transversal crossing two lines. They use formulas for the area and perimeter of rectangles and calculate volumes of rectangular prisms. Students classify triangles and quadrilaterals. They name the types of angles formed by a transversal crossing parallel lines.
Statistics and Probability
Students identify issues involving the collection of continuous data. They construct stem-and-leaf plots and dot plots. Students describe the relationship between the median and mean in data displays. They calculate mean, mode, median and range for data sets. Students determine the sample space for simple experiments with equally likely outcomes and assign probabilities to those outcomes.
Year 8 Syllabus
Year Level Description
The proficiency strands understanding, fluency, problem-solving and reasoning are an integral part of mathematics content across the three content strands: number and algebra, measurement and geometry, and statistics and probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics. The achievement standards reflect the content and encompass the proficiencies.
At this year level:
- understanding includes describing patterns involving indices and recurring decimals, identifying commonalities between operations with algebra and arithmetic, connecting rules for linear relations with their graphs, explaining the purpose of statistical measures and explaining measurements of perimeter and area
- fluency includes calculating accurately with simple decimals, indices and integers; recognising equivalence of common decimals and fractions including recurring decimals; factorising and simplifying basic algebraic expressions and evaluating perimeters and areas of common shapes and volumes of three-dimensional objects
- problem-solving includes formulating and modelling practical situations involving ratios, profit and loss, areas and perimeters of common shapes and using two-way tables and Venn diagrams to calculate probabilities
- reasoning includes justifying the result of a calculation or estimation as reasonable, deriving probability from its complement, using congruence to deduce properties of triangles, finding estimates of means and proportions of populations.
Number and Algebra
Number and place value
Use index notation with numbers to establish the index laws with positive integral indices and the zero index (ACMNA182)
Carry out the four operations with rational numbers and integers, using efficient mental and written strategies and appropriate digital technologies (ACMNA183)
Real numbers
Investigate terminating and recurring decimals (ACMNA184)
Investigate the concept of irrational numbers, including π (ACMNA186)
Solve problems involving the use of percentages, including percentage increases and decreases, with and without digital technologies (ACMNA187)
Solve a range of problems involving rates and ratios, with and without digital technologies (ACMNA188)
Money and financial mathematics
Solve problems involving profit and loss, with and without digital technologies (ACMNA189)
Patterns and algebra
Extend and apply the distributive law to the expansion of algebraic expressions (ACMNA190)
Factorise algebraic expressions by identifying numerical factors (ACMNA191)
Simplify algebraic expressions involving the four operations (ACMNA192)
Linear and non-linear relationships
Plot linear relationships on the Cartesian plane with and without the use of digital technologies (ACMNA193)
Solve linear equations using algebraic and graphical techniques. Verify solutions by substitution (ACMNA194)
Measurement and Geometry
Using units of measurement
Choose appropriate units of measurement for area and volume and convert from one unit to another (ACMMG195)
Find perimeters and areas of parallelograms, trapeziums, rhombuses and kites (ACMMG196)
Investigate the relationship between features of circles such as circumference, area, radius and diameter. Use formulas to solve problems involving circumference and area (ACMMG197)
Develop formulas for volumes of rectangular and triangular prisms and prisms in general. Use formulas to solve problems involving volume (ACMMG198)
Solve problems involving duration, including using 12- and 24-hour time within a single time zone (ACMMG199)
Geometric reasoning
Define congruence of plane shapes using transformations (ACMMG200)
Develop the conditions for congruence of triangles (ACMMG201)
Establish properties of quadrilaterals using congruent triangles and angle properties, and solve related numerical problems using reasoning (ACMMG202)
Statistics and Probability
Chance
Identify complementary events and use the sum of probabilities to solve problems (ACMSP204)
Describe events using language of 'at least', exclusive 'or' (A or B but not both), inclusive 'or' (A or B or both) and 'and' (ACMSP205)
Represent events in two-way tables and Venn diagrams and solve related problems (ACMSP292)
Data representation and interpretation
Investigate techniques for collecting data, including census, sampling and observation (ACMSP284)
Explore the practicalities and implications of obtaining data through sampling using a variety of investigative processes (ACMSP206)
Explore the variation of means and proportions of random samples drawn from the same population (ACMSP293)
Investigate the effect of individual data values, including outliers, on the mean and median (ACMSP207)
Year 8 Achievement Standard
Number and Algebra
At Standard, students solve everyday problems involving rates, ratios and percentages. They describe index laws and apply them to whole numbers. Students describe rational and irrational numbers. They solve problems involving profit and loss. Students make connections between expanding and factorising algebraic expressions. They use efficient mental and written strategies to carry out the four operations with integers. Students simplify a variety of algebraic expressions. They solve linear equations and graph linear relationships on the Cartesian plane.
Measurement and Geometry
Students solve problems relating to the volume of prisms. They make sense of time duration in real applications. Students identify conditions for the congruence of triangles and deduce the properties of quadrilaterals. They convert between units of measurement for area and volume. Students perform calculations to determine perimeter and area of parallelograms, rhombuses and kites. They name the features of circles and calculate the areas and circumferences of circles.
Statistics and Probability
Students model authentic situations with two-way tables and Venn diagrams. They choose appropriate language to describe events and experiments. Students explain issues related to the collection of data and the effect of outliers on means and medians in that data. They determine the probabilities of complementary events and calculate the sum of probabilities.
Year 9 Syllabus
Year Level Description
The proficiency strands understanding, fluency, problem-solving and reasoning are an integral part of mathematics content across the three content strands: number and algebra, measurement and geometry, and statistics and probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics. The achievement standards reflect the content and encompass the proficiencies.
At this year level:
- understanding includes describing the relationship between graphs and equations, simplifying a range of algebraic expressions and explaining the use of relative frequencies to estimate probabilities and of the trigonometric ratios for right-angle triangles
- fluency includes applying the index laws to expressions with integer indices, expressing numbers in scientific notation, listing outcomes for experiments, developing familiarity with calculations involving the Cartesian plane and calculating areas of shapes and surface areas of prisms
- problem-solving includes formulating and modelling practical situations involving surface areas and volumes of right prisms, applying ratio and scale factors to similar figures, solving problems involving right-angle trigonometry and collecting data from secondary sources to investigate an issue
- reasoning includes following mathematical arguments, evaluating media reports and using statistical knowledge to clarify situations, developing strategies in investigating similarity and sketching linear graphs.
Number and Algebra
Real numbers
Solve problems involving direct proportion. Explore the relationship between graphs and equations corresponding to simple rate problems (ACMNA208)
Apply index laws to numerical expressions with integer indices (ACMNA209)
Express numbers in scientific notation (ACMNA210)
Money and financial mathematics
Solve problems involving simple interest (ACMNA211)
Patterns and algebra
Extend and apply the index laws to variables, using positive integer indices and the zero index (ACMNA212)
Apply the distributive law to the expansion of algebraic expressions, including binomials, and collect like terms where appropriate (ACMNA213)
Linear and non-linear relationships
Find the distance between two points located on the Cartesian plane using a range of strategies, including graphing software (ACMNA214)
Find the midpoint and gradient of a line segment (interval) on the Cartesian plane using a range of strategies, including graphing software (ACMNA294)
Sketch linear graphs using the coordinates of two points and solve linear equations (ACMNA215)
Graph simple non-linear relations with and without the use of digital technologies and solve simple related equations (ACMNA296)
Measurement and Geometry
Using units of measurement
Calculate areas of composite shapes (ACMMG216)
Calculate the surface area and volume of cylinders and solve related problems (ACMMG217)
Solve problems involving the surface area and volume of right prisms (ACMMG218)
Investigate very small and very large time scales and intervals (ACMMG219)
Geometric reasoning
Use the enlargement transformation to explain similarity and develop the conditions for triangles to be similar (ACMMG220)
Solve problems using ratio and scale factors in similar figures (ACMMG221)
Pythagoras and trigonometry
Investigate Pythagoras’ Theorem and its application to solving simple problems involving right-angled triangles (ACMMG222)
Use similarity to investigate the constancy of the sine, cosine and tangent ratios for a given angle in right-angled triangles (ACMMG223)
Apply trigonometry to solve right-angled triangle problems (ACMMG224)
Statistics and Probability
Chance
List all outcomes for two-step chance experiments, both with and without replacement using tree diagrams or arrays. Assign probabilities to outcomes and determine probabilities for events (ACMSP225)
Calculate relative frequencies from given or collected data to estimate probabilities of events involving 'and' or 'or' (ACMSP226)
Investigate reports of surveys in digital media and elsewhere for information on how data were obtained to estimate population means and medians (ACMSP227)
Data representation and interpretation
Identify everyday questions and issues involving at least one numerical and at least one categorical variable, and collect data directly and from secondary sources (ACMSP228)
Construct back-to-back stem-and-leaf plots and histograms and describe data, using terms including ‘skewed’, ‘symmetric’ and ‘bi modal’ (ACMSP282)
Compare data displays using mean, median and range to describe and interpret numerical data sets in terms of location (centre) and spread (ACMSP283)
Year 9 Achievement Standard
Number and Algebra
At Standard, students solve problems involving simple interest. They apply the index laws to numbers and express numbers in scientific notation. Students expand binomial expressions. They find the distance between two points on the Cartesian plane and the gradient and midpoint of a line segment. Students sketch linear and non-linear relations.
Measurement and Geometry
Students interpret ratio and scale factors in similar figures. They explain similarity of triangles. Students recognise the connections between similarity and the trigonometric ratios. They calculate areas of shapes and the volume and surface area of right prisms and cylinders. Students use Pythagoras’ Theorem and trigonometry to find unknown sides of right-angled triangles.
Statistics and Probability
Students calculate relative frequencies to estimate probabilities, list outcomes for two-step experiments and assign probabilities for those outcomes. They compare techniques for collecting data from primary and secondary sources. Students construct histograms and back-to-back stem-and-leaf plots. They make sense of the position of the mean and median in skewed, symmetric and bi-modal displays to describe and interpret data.
Year 10 Syllabus
Year Level Description
The proficiency strands understanding, fluency, problem-solving and reasoning are an integral part of mathematics content across the three content strands: number and algebra, measurement and geometry, and statistics and probability. The proficiencies reinforce the significance of working mathematically within the content and describe how the content is explored or developed. They provide the language to build in the developmental aspects of the learning of mathematics. The achievement standards reflect the content and encompass the proficiencies.
At this year level:
- understanding includes applying the four operations to algebraic fractions, finding unknowns in formulas after substitution, making the connection between equations of relations and their graphs, comparing simple and compound interest in financial contexts and determining probabilities of two- and three-step experiments
- fluency includes factorising and expanding algebraic expressions, using a range of strategies to solve equations and using calculations to investigate the shape of data sets
- problem-solving includes calculating the surface area and volume of a diverse range of prisms to solve practical problems, finding unknown lengths and angles using applications of trigonometry, using algebraic and graphical techniques to find solutions to simultaneous equations and inequalities and investigating independence of events
- reasoning includes formulating geometric proofs involving congruence and similarity, interpreting and evaluating media statements and interpreting and comparing data sets.
Number and Algebra
Money and financial mathematics
Connect the compound interest formula to repeated applications of simple interest using appropriate digital technologies (ACMNA229)
Patterns and algebra
Factorise algebraic expressions by taking out a common algebraic factor (ACMNA230)
Simplify algebraic products and quotients using index laws (ACMNA231)
Apply the four operations to simple algebraic fractions with numerical denominators (ACMNA232)
Expand binomial products and factorise monic quadratic expressions using a variety of strategies (ACMNA233)
Substitute values into formulas to determine an unknown (ACMNA234)
Linear and non-linear relationships
Solve problems involving linear equations, including those derived from formulas (ACMNA235)
Solve linear inequalities and graph their solutions on a number line (ACMNA236)
Solve linear simultaneous equations, using algebraic and graphical techniques, including using digital technology (ACMNA237)
Solve problems involving parallel and perpendicular lines (ACMNA238)
Explore the connection between algebraic and graphical representations of relations such as simple quadratics, circles and exponentials using digital technology as appropriate (ACMNA239)
Solve linear equations involving simple algebraic fractions (ACMNA240)
Solve simple quadratic equations using a range of strategies (ACMNA241)
Measurement and Geometry
Using units of measurement
Solve problems involving surface area and volume for a range of prisms, cylinders and composite solids (ACMMG242)
Geometric reasoning
Formulate proofs involving congruent triangles and angle properties (ACMMG243)
Apply logical reasoning, including the use of congruence and similarity, to proofs and numerical exercises involving plane shapes (ACMMG244)
Pythagoras and trigonometry
Solve right-angled triangle problems including those involving direction and angles of elevation and depression (ACMMG245)
Statistics and Probability
Chance
Describe the results of two- and three-step chance experiments, both with and without replacements, assign probabilities to outcomes and determine probabilities of events. Investigate the concept of independence (ACMSP246)
Use the language of ‘if ....then', ‘given’, ‘of’, ‘knowing that’ to investigate conditional statements and identify common mistakes in interpreting such language (ACMSP247)
Data representation and interpretation
Determine quartiles and interquartile range (ACMSP248)
Construct and interpret box plots and use them to compare data sets (ACMSP249)
Compare shapes of box plots to corresponding histograms and dot plots (ACMSP250)
Use scatter plots to investigate and comment on relationships between two numerical variables (ACMSP251)
Investigate and describe bivariate numerical data where the independent variable is time (ACMSP252)
Evaluate statistical reports in the media and other places by linking claims to displays, statistics and representative data (ACMSP253)
Year 10 Achievement Standard
Number and Algebra
At Standard, students recognise the connection between simple and compound interest. They solve problems involving linear equations and inequalities. Students make the connections between algebraic and graphical representations of relations. They expand binomial expressions and factorise monic quadratic expressions. Students find unknown values after substitution into formulas. They perform the four operations with simple algebraic fractions. Students solve simple quadratic equations and pairs of simultaneous equations.
Measurement and Geometry
Students solve surface area and volume problems relating to composite solids. They recognise the relationships between parallel and perpendicular lines. Students apply deductive reasoning to proofs and numerical exercises involving plane shapes. They use triangle and angle properties to prove congruence and similarity. Students use trigonometry to calculate unknown angles in right-angled triangles.
Statistics and Probability
Students compare data sets by referring to the shapes of the various data displays. They describe bivariate data where the independent variable is time. Students describe statistical relationships between two continuous variables. They evaluate statistical reports. Students list outcomes for multi-step chance experiments and assign probabilities for these experiments. They calculate quartiles and inter-quartile ranges.
Year 10A Syllabus
Number and Algebra
Real numbers
Define rational and irrational numbers and perform operations with surds and fractional indices (ACMNA264)
Use the definition of a logarithm to establish and apply the laws of logarithms (ACMNA265)
Patterns and algebra
Investigate the concept of a polynomial and apply the factor and remainder theorems to solve problems (ACMNA266)
Linear and non-linear relationships
Describe, interpret and sketch parabolas, hyperbolas, circles and exponential functions and their transformations (ACMNA267)
Solve simple exponential equations (ACMNA270)
Apply understanding of polynomials to sketch a range of curves and describe the features of these curves from their equation (ACMNA268)
Factorise monic and non-monic quadratic expressions and solve a wide range of quadratic equations derived from a variety of contexts (ACMNA269)
Measurement and Geometry
Using units of measurement
Solve problems involving surface area and volume of right pyramids, right cones, spheres and related composite solids (ACMMG271)
Geometric reasoning
Prove and apply angle and chord properties of circles (ACMMG272)
Pythagoras and trigonometry
Establish the sine, cosine and area rules for any triangle and solve related problems (ACMMG273)
Use the unit circle to define trigonometric functions, and graph them with and without the use of digital technologies (ACMMG274)
Solve simple trigonometric equations (ACMMG275)
Apply Pythagoras’ Theorem and trigonometry to solving three-dimensional problems in right-angled triangles (ACMMG276)
Statistics and Probability
Chance
Investigate reports of studies in digital media and elsewhere for information on their planning and implementation (ACMSP277)
Data representation and interpretation
Calculate and interpret the mean and standard deviation of data and use these to compare data sets (ACMSP278)
Use information technologies to investigate bivariate numerical data sets. Where appropriate use a straight line to describe the relationship allowing for variation (ACMSP279)
Achievement standard
To be developed using (assessment) work sample evidence to ‘set’ standards through paired comparisons.
