Year 9
Mathematics Support Materials
Mathematics snapshot: Pythagoras’ Theorem
Mathematics/Measurement and Geometry/Pythagoras and trigonometry
| Content Description | Relevant aspects of the Achievement Standards |
|---|---|
|
Investigate Pythagoras’ Theorem and its application to solving simple problems involving right angled triangles (ACMMG222) Apply trigonometry to solve right-angled triangle problems (ACMMG224) |
Students use Pythagoras’ Theorem and trigonometry to find unknown sides of right-angled triangles |
Nature of the assessment
Anecdotal evidence based on teacher observation
Purposes of the assessment
To assess the students’ ability to identify and use an appropriate model to determine unknown lengths and angles in right triangles.
Stage in the teaching sequence
Towards the end of a lesson sequence
Assessment task 1
The students were required to solve each of the following problems.
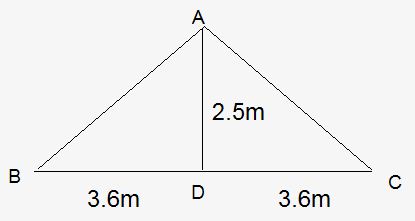
1. A pergola is to be built with a gabled roof as shown.
What is the length of AB, the slant height of the gable?
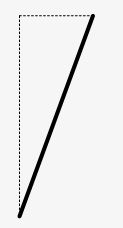
2. A footing underneath a 65 m tall building has become unstable and, as a result, the building currently leans at an angle of 4 to the vertical (as shown below). Determine the vertical distance.
Assessment process
Working in pairs, the students had to decide whether each problem could be solved using Pythagoras’ Theorem or trigonometry, based on the key information in each scenario. The students were then required to apply the appropriate model and determine the length of the unknown side in question.
Assessment task 2
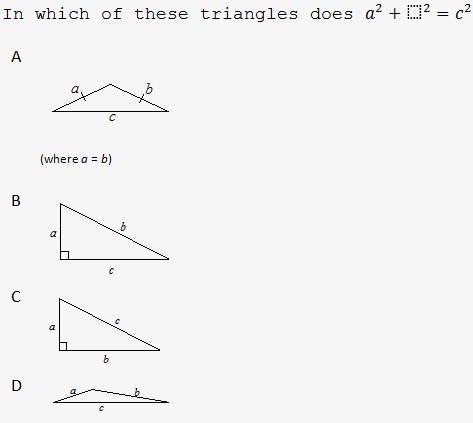
The teacher ended the lesson by posing the following question.
Students held up an A, B, C, D card to show their response.
Using the information
The multiple-choice question showed that all students selected B or C indicating they knew that Pythagoras’ Theorem only applied to right-angled triangles. Based on her observations from both assessments, the teacher identified she needed to give specific students more practice with applying Pythagoras’ Theorem and trigonometry to a variety of scenarios. She also determined that some students were still having problems with rearranging terms when solving equations involved in the solution of these types of problems. She used this information to plan her next lesson.
Overview of research
View the overview of research for this snapshot.